Your Temperature Measurement Experts
Technical Papers
Errors Related to Cable Resistance Imbalance in Three Wire RTDs
There are multiple sources of error that can impact the accuracy of an RTD measurement. The cable incorporated into the sensor can cause a significant error. In this paper an analysis of cable resistance imbalance in three wire resistance temperature detectors (RTDs) is presented with emphasis on the errors that can result in the temperature measurement. Guidance and techniques are given for minimizing the magnitude of these errors.
Common Sources of Error in RTD Selection and Installation:
- Interchangeability
- Stability
- Hysteresis
- Calibration/interpolation
- Self Heating
- Thermal EMF
- Insulation Resistance
- Repeatability
- Stem conduction
- Lead Wire
- Time Response
Background
RTDs are temperature sensors that utilize the predictable change in electrical resistance of a material (typically platinum) with changing temperature. To provide a practical temperature measuring instrument it is necessary to attach extension leads to the platinum sensing element. If not properly selected for the application the number and type of extension leads used can introduce significant errors into the temperature measurement. See Figure 1 for the different connection methods.
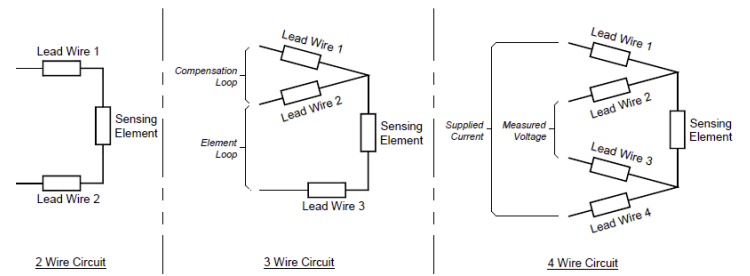
Figure 1. Temperature Sensor Lead Wire Configuration
Two Wire RTD
The two lead wire circuit has no mechanism to compensate or eliminate the resistance of the lead wires from the resistance of the element. The two lead wire design is only useful when the extension lead resistance is insignificant compared to the sensing element resistance; either the leads are very short or the sensing element resistance is large.
Three Wire RTD
The three wire configuration provides a compensation loop that can be used to subtract the lead wire resistance from the resistance measurement of the element loop, resulting in a value for just the element resistance. As will be shown, achieving an accurate measurement with this method is predicated on the resistance of each of the leads being exactly equal. Unfortunately this is seldom the case, and steps must be taken in the design and application of a three wire sensor to maintain the accuracy of the measurement.
True Four Wire RTD
The method that offers the highest accuracy temperature measurement is the true four wire sensor design. A sensor circuit with two wires on each side of the element allows for a measurement current to be passed across the element via two of the leads and a voltage measurement to be taken through the other two leads. The resistance is simply then calculated using Ohms law (V=IR or R=V/I). The impedance of the meter taking the voltage measurement is sufficiently high to prevent any current from flowing through the leads being used for the voltage measurement. The current flowing through the other two leads and the element is the same throughout the circuit. Therefore by measuring the voltage across the element and dividing it by the known current yields just the resistance of the element.
Unfortunately it is not always practical or feasible to use the four wire method and often the method selected is the three wire method.
Alternate 4-Wire Sensor Style: Compensation Loop
There is an alternate 4-wire version that essentially combines a 2-wire hook up and a compensation loop that runs the length of the sensor yet is NOT attached to the element. This style generally will behave similar to the 3-wire regarding the potential imbalance affect. It is important to be aware of which 4-wire design is utilized in the selection of an RTD.
Three Wire Measurement Theory
Essentially to provide a three wire temperature measurement it is necessary to measure the resistance of the element loop and subtract the resistance of the compensation loop.
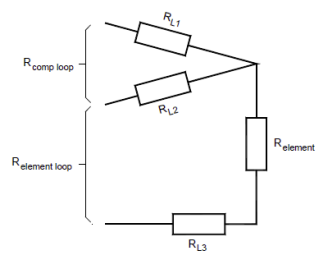
Figure 2. Three Wire Circuit
From Figure 2. the resistance of the lead wires and element are in series:
- So; Relement loop = RL2 + Eelement + RL3
- And; Rcomp loop = RL1 + RL2
- Subtracting Relement loop – Rcomp loop
- Yields; Relement loop – Rcomp loop = (RL2 + Relement + RL3) – (RL1 + RL2)
- Assuming that RL1 = RL2 = RL3 then the lead resistances cancel out and
- Relement loop – Rcomp loop = Relement
In practice however the theoretical assumption that RL1 = RL2 = RL3 is rarely true. Within any set of wires, there is always some difference (an imbalance) in these values. This imbalance results in the residual difference between RL1, RL2, and RL3 being included in the measurement of Relement resulting in an offset in the element resistance and therefore in the resulting temperature measured.
Typically the sensor manufacturer will use one lead color for RL3 and another lead color for both RL1 and RL2 (i.e. RL1 and RL2 will be the same color). If the resistance imbalance is large between R L1 and R L2 , then depending on which way these seemingly interchangeable leads are connected to the readout in the field, a significant error can result in the temperature measurement.
Sources of the Cable Resistance Imbalance
The resistance of a conductor (R) is based on the formula:
R = ρ * L/A
Where ρ = resistivity, a constant for a particular material at a particular temperature (Ω ft)
L = length of the conductor (ft)
A = Cross-sectional-area of the conductor (ft2)
As the length increases and/or the diameter decreases the resistance of the conductor increases. To maintain flexibility, cables are usually manufactured from multiple drawn strands of thin wire that are twisted together to form a conductor of the correct diameter for the particular wire gauge size. The bare twisted strand conductor is then insulated. Several insulated conductors are twisted together to form the cable, then an insulating and protective jacket is applied over the twisted conductors.
diameter decreases the resistance of the conductor increases. To maintain flexibility, cables are usually manufactured from multiple drawn strands of thin wire that are twisted together to form a conductor of the correct diameter for the particular wire gauge size. The bare twisted strand conductor is then insulated. Several insulated conductors are twisted together to form the cable, then an insulating and protective jacket is applied over the twisted conductors.
Each one of these steps involves de-reeling the wire, passing it through a series of tensioning pulleys through the process and then spooling it back onto another reel before it goes onto the next step. This processing of the wire, despite the best efforts of the cable manufacturers, causes the conductors to stretch. The stretching of the cable results in a reduction in cross sectional area and thus an increase in cable resistance. From lot to lot it is difficult to consistently control the stretching. Typically the conductors that make up the cable come from different production runs. Ultimately when the different conductors are brought together to form the cable they have slightly different cross-sectional-areas, although still within the standard for the gauge size, but resulting in an imbalance in their resistances.
In the case of copper conductors, the copper is typically plated with silver or nickel to improve the corrosion resistance. The overall resistance of the conductor is a function of the resistivity of the two materials and their corresponding cross sectional areas. Unfortunately thickness control in the plating process is difficult. Any variation in the thickness results in a variation in the cross-sectional area. When the resistivity of the plating material is high this problem is exacerbated.
Nickel is a common plating material used for copper conductors and has a resistivity much higher than the copper. So a variation in thickness of the nickel results in a larger variation in the resistivity of the conductor.
Another common plating material for copper is silver, which has a lower resistivity than nickel. Any variation in the thickness of the coating of the silver has much less of an effect on the conductor resistivity compared to what a similar variation in nickel plating would have. However there are cost, corrosion and temperature constraints that have to be considered when selecting silver rather than nickel.
Magnitude of the Imbalance in the Cable
For applications where circuit resistance is not important to the function, the imbalance in the conductors of the cable is not significant enough to cause a problem. Basically the ASTM standards only specify the cross-sectional area of the conductor and the plating thickness. The variation allowed in the Standards, yields a range in wire resistance greater than the three wire RTD compensation method can accept. Most cable manufacturers are able to do much better than what the ASTM standards dictate. One cable manufacturer we have consulted with states that a maximum variation of 4% in resistivity for silver plated wire and 11% for nickel plated wire is considered achievable.
To highlight the issue, consider the example of a Class A temperature sensor built with 30 feet of 30 AWG nickel plated copper cable.
- A 30 AWG conductor has a resistivity of 99.2 Ω/1000ft, so for a 30’ sensor cable the resistance of each conductor will be 2.976 Ω. Assuming the 11% achievable matching value, the variation between conductors could be as much as 0.327 Ω.
- A “class A” sensor at the ice point (0.0 ºC) has a resistance of 100 ±0.060 Ω. Typically a “class A” sensor will be built utilizing an element with an initial ice point resistance tighter than the Class A tolerance to allow for slight variation due to the manufacturing process. Clearly there is no room in the tolerance budget to support the potential imbalance of 0.327 Ω. In terms of temperature, the tolerance at the ice point for a Class A sensor is; 0.0 ± 0.156 ºC. The imbalance in the cable conductors (0.327 Ω) will cause an additional error of approximately 0.85ºC effectively resulting in a three wire sensor with an ice point accuracy 6 time larger than the design target, or approximately 0.0 ± 1°C.
Methods to Mitigate the Errors from Cable Imbalance
Steps can be taken to mitigate the problem of cable imbalance in a three wire temperature sensor. The list below gives an overview of each of the options. Typically some compromise needs to be made in order to reduce the effect of cable imbalance.
- Switch from a three wire sensor to a true four wire sensor. A true four wire measurement negates any effect of lead wire resistance and thus will always give a superior measurement. It is not always possible to switch to a four wire configuration, sometimes due to space constraints in the probe or because the existing control or meter infrastructure is configured for three wire sensors.
- Increase the cable gauge. For a three wire measurement the cable conductor gauge used should be as large as possible. As seen earlier the larger the cable gauge the lower the resistance and the lower the imbalance in the conductors in the cable. Space constraints inside the RTD often do not allow for a larger cable size. Even with a larger cable there will be a cable length at which the possible cable resistance imbalance will result in the sensor being out of its accuracy tolerance.
- Splice to a larger cable outside the RTD. If space constraints internal to the RTD prevent incorporating a larger cable size then a larger cable can be spliced to the small cable outside of the sensor. In the area of the splice the cable will be stiffer and will have a slightly larger diameter than either of the cables. This may make it difficult to pass the cable through conduit. Again even with a larger cable gauge in the circuit there is still a cable length at which the possible cable resistance imbalance will result in the sensor being out of its accuracy tolerance.
- Resistance Trim the cable and fix the length. The cable can be balanced by adding a compensation resistance to the appropriate conductor(s) in the cable. Typically, the compensation resistance is added near the end of the cable to keep it away from process temperatures. To maintain the accuracy of the temperature sensor it is important that the cable is not cut during installation as this will physically remove the compensation resistance and return the cable to its original unbalanced state.
- Switch to a silver plated copper cable. By switching from a nickel plated copper to a silver plated copper cable will allow for longer cable lengths. Silver has a lower temperature rating and does not do particularly well in moist environments.
Conclusion
A high accuracy temperature measurement requires a true four wire sensor. When the application will not allow for a four wire sensor a three wire sensor can be utilized but the end user should be aware of how the accuracy is potentially being affected by the three wire circuitry. Some probe manufacturers do not address the issue of degradation of measurement accuracy with reduced cable gauges and/or longer cable lengths; however the cable imbalance issue is always present. By taking into consideration the effects of cable imbalance at the time a three wire sensor is specified, and by carefully evaluating and selecting one of the techniques to reduce the effect of cable resistance imbalance, it is possible to produce a three wire measurement probe that will provide a temperature measurement at the needed accuracy.
